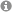Anderson Transitions and Quantum Criticality in Novel Materials: Topological Insulators, Graphene and Friends

The Anderson transition is a kind of metal-to-insulator transition that can occur in a metallic material, if the concentration of impurities exceeds a critical threshold. The phenomenon owes its interest to the fact that it is caused by quantum interference which can completely inhibit the otherwise diffusive motion of free charge carriers under certain conditions at low enough temperatures. Since the transition is driven by disorder and occurs only at zero temperature it qualifies as a particular kind of quantum-phase transition.

Even though localization and related physics are already a traditional subject of fundamental condensed matter research, still new and sometimes very surprising phenomena are being discovered. Amongst the most recent topics is the peculiar suppression of localization in graphene, which could lead to as yet unobserved novel quantum critical behavior. Also in topological materials new kinds of Anderson-transitions are suspected to exist and hopefully become experimentally observable in the foreseeable future. In this way insights obtained in this field relate to technological applications as well as to other directions of fundamental research, e.g., quantum computing.

Our research in the matter has a special focus on the following two key aspects:
?

Aspects of Multifractality at the Metal-Insulator-Transition

Wavefunction of a graphene lattice with vacancies. The logarithmic color coding exhibits the large amplitude fluctuations that are the hallmark of (nearly "frozen") multifractality in this system. ? ?

One of the particularly beautiful aspects of the critical state relates to the amplitude distribution of the associated wavefunctions. Since such wavefunctions live right at the boundary between a metal and an insulator, they have very peculiar properties. In particular, they exhibit an unusual type of self-similarity that is called "multi-fractality". A fractal structure has the property that it fills only a certain fraction of the embedding space, so that it carries a fractal dimension that is lower than the dimension of the embedding. Wavefunctions at the Anderson-transition are multi-fractal, because different moments of their amplitude each carry their own specificfractal dimension. We study the associated set of exponents, the multi-fractal spectrum, because it contains essential information about the nature and classification of the transition - but also, because current experimental efforts are promising so that hopefully such spectra can also be measured, soon. Our most current example is graphene, that exhibits multifractality in the presence of vacancy-disorder (if treated on a tight binding level).

Have a look at the Anderson transition in graphene in our Physical Review Letters article.

????

Classification Scheme and Critical Fixed Points: Anderson Transitions

Quantum interference is sensitive to basic symmetries, most notably time reversal, spin rotations and other, less obvious ones,like "chiral" symmetries. Therefore, many different kinds of Anderson-insulators exist the most famous one being the quantum-Hall insulator. Even though in the last years the "periodic table" of dirty-metal phases has been completed, the properties of these phases and in particular the possible transitions between them are still largely unexplored and often poorly understood. Our numerical effort is devoted to shed more light into this intricate and fascinating world of localization-induced quantum criticality. Many different methods are developed and employed for this purpose in our group. They include transfer-matrices, wave-function propagation with Krylov-space methods and Lanczos-type of techniques and many others...
?
Learn more about Anderson transitions in our Reviews of Modern Physics article.

???