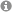Open projects for students

We are always looking for motivated students to join our group. If you are looking for a Bachelor's or Master's thesis in the field of Computational Condensed Matter Theory, please contact Prof. F. Evers or Dr. J. Wilhelm. Please find exemplary projects below.

Master Thesis on Molecular Machines

A molecular machine is a large molecule that undergoes a (directed) rotation when an electric current flows through. A candidate molecule for such a device is a helix as sketched below. Helical molecules can nowadays be synthesized in the laboratory [1]. Within a classical picture the directionality of the rotation results from angular momentum conservation.

In?this Master project, we propose to calculate how the electric current flows through such helical molecules. To this end, the inhouse transport software package aitranss [2-3] will be equipped with a fresh module to calculate the current density, j(r). Resorting to an argument from classical mechanics, the mechanical torque exerted on the molecule by the current flow will be accessible. As an application, we propose to study effects of the precise molecular geometry on the angular momentum gain of the molecule, e.g., to estimate the efficiency of potential molecular machines.

For the Master thesis, first experiences in electronic structure theory will be benefitial. E.g. having attended the lectures “Computational Nanoscience” or “Computational Electronic Structure Theory of Solids” will be helpful, but is certainly not a required prerequisite. During the Master thesis, we offer close mentoring and a hands-on introduction to electronic structure calculations and our transport package. As a bonus, you will get first experience in contributing to larger software packages and joint software development.

[1] M. Rickhaus et al., Angew. Chem. Int. Ed. 53, 14587 (2014)
[2] A. Arnold et al., J. Chem. Phys. 126, 174101 (2007)
[3] J. Wilhelm et al., Phys. Rev. B 89, 195406 (2014)
? ??

? ? ? ? ? ? ? ? ? ? ? ? ? ??

High-harmonic generation in topological insulators

When irradiating a solid with ultra-short laser pulses (duration ~ 100 fs), electrons are excited from valence bands to conduction bands. The electric field of the laser pulse

???????????????? E(t) = E₀ cos?(ωt) exp?(?t?/σ?)

features a Gaussian envelope and is typically modulated with an oscillating frequency? ω in the Terahertz range [1]. From a driven harmonic oscillator, we expect the charge density to also oscillate with a frequency ω as response to the electric field. However, due to multiple excitation of electrons between bands and due to acceleration of already excited electrons by the electric field E(t), the electron charge density oscillates not only with frequency ω, but also with higher frequencies nω, n∈N. Consequently, the emitted radiation by the charge density movement features high-harmonic frequencies nω, where n>20 can be observed.

In the project "Effects of interactions on high harmonic generation in topological insulators", we propose to extend our semiconductor Bloch equations code (https://github.com/ccmt-regensburg/CUED, [2]) to capture Coulomb interactions of the involved charge carriers. Once having the coding part finalized, we propose to investigate the effects of Coulomb interactions on the high-harmonic spectrum using the developed code.

[1] C. P. Schmid et al., Nature 593, 385-390 (2021)
[2] J. Wilhelm et al., Phys. Rev. B 103, 125419 (2021)

Dynamics in quantum many-body models bridging between model-based theory and microscopic realism

Tips and tricks??

You can find some tips and tricks when working in the computational condensed matter theory group here?(internal).