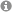Machine learning of the Hartree potential

??????
In many applications, TDDFT simulations of electron dynamics come with an enormous computational cost. Two reasons are as follows: First, time steps as short as a few attoseconds are required which leads to tens of thousands of time steps for simulating a typical laser pulse with a duration of 100 fs. Second, atomistic models with hundreds of atoms are often necessary to prevent finite-size effects, for example in the field of nanoplasmonics [1] where typically, a large metallic nanostructe needs to be considered, see below sketch (a) of a metallic tip on a metallic surface.

The starting point for the highly efficient TDDFT algorithm is the TDDFT implementation in the CP2K package [2] which is optimized for massively parallel execution on supercomputers. The computational bottleneck of TDDFT is the calculation of the Hartree potential from the density matrix. This operation is repeated in every TDDFT time step for similar input density matrices. Machine learning (ML) models will be trained for a cheap computation of the Hartree potential from the density matrix, see sketch (b) and (c) below. The best accuracy of the ML model is expected when incorporating as much available information as possible. Such information may include for example the Hartree potential from previous time steps or information on the shape of the Gaussian basis. The ML algorithm for evaluating the Hartree potential from the density matrix will be applicable to any atom type in any material. Moreover, the ML algorithm can be also used in ground-state ab-initio molecular dynamics simulations for calculating the Hartree potential from the density matrix which might be interesting for many CP2K users.?
? ? ? ? ?
[1] See "10. Quantum plasmonics" in Stockman?et al.,?Roadmap on plasmonics,?J. Opt.?20, 043001 (2018).

[2]?T. D. Kühne et al.,?CP2K: An electronic structure and molecular dynamics software package - Quickstep: Efficient and accurate electronic structure calculations, J. Chem. Phys. 152, 194103 (2020).