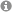Parametrized Automata

Parametrized Automata (PA) are a model of computation that extends Finite-State Automata in order to be suitable for languages over infinite alphabets. As such, PA have been previously utilized in investigating the decision properties of sequence theories [1] and the study of data words [2] and combine traits from two better-known classes of automata.

The first are Symbolic Automata [3], whose transitions are labeled with logical formulas instead of letters, meaning the properties of Symbolic Automata are often very similar to those of Finite-State Automata.

In the depicted Symbolic Automaton, the variable x functions as a placeholder for the current letter. As such, the automaton accepts all words that have a prefix consisting solely of even numbers followed by a number larger than 5.

The second are Variable Automata [4], which compare input letters to a finite set of variables and as such, can compare input letters for equality and inequality.

The Variable Automaton in the figure employs a variable y which can be assigned a random letter. The free variable z represents all letters not stored in y. Over all possible variable assignments, the automaton therefore accepts all words in which some letter occurs twice.

In PA, each transition is labeled with a logical formula which may also contain parameters drawn from a finite set.

As before, x represents the current letter while the parameter y can be assigned some arbitrary but fixed letter. Therefore, the first example PA accepts all words where the last letter is strictly the largest, and the second example PA accepts all words whose letters fall within an interval of length 1.

Closure properties

PA are closed under intersection and union, but not under complementation. An example of a PA which cannot be complemented is the PA identifying unsorted words, and its non-complementability can be proven by utilizing the pumping lemma for PA.

Decision problems

While problems like non-emptiness of PA or the reachability of states are decidable for PA, the universality problem is not, leading to a number of other limitations of PA. Namely, the problem of either complementing a given PA, or returning that such a complement does not exist, is also undecidable.

Determinism in PA

There is no straightforward way of lifting the definition of determinism from Finite-State Automata to PA. A Finite-State Automaton is deterministic if every word completes exactly one run through the automaton or if for every state and letter, there is exactly one exiting transition, and both of these definitions coincide. In PA, these definitions lead to different notions of determinism.

Determinism per assignment

We call a PA deterministic per assignment if for every state, letter and parameter assignment, there is exactly one exiting transition. For every PA, an equivalent PA that is deterministic per assignment can be computed algorithmically. Determinism per assignment is useful for a number of other operations, such as product constructions or minimization of PA. An example:

Strongly deterministic Parametrized Automata

A PA is strongly deterministic, or an SDPA, if every word completes exactly one run. Not every complementable PA can be transformed into an SDPA, yet strong determinism allows for easy complementation.

Both automata depicted represent the same language of all words in which the first letter is strictly the largest. The first automaton is strongly deterministic, while the second is deterministic per assignment.

Complementable Normal Form

A PA is in Complementable Normal Form, or a CFPA, if there is a subset of states accepting the PA’s complement language. Every complementable PA is equivalent to some CFPA, but since the generalized complementation problem is undecidable, there is likely no algorithmic approach to always find such a CFPA.

Depicted is a CFPA where the states marked in red accept the original language and the state marked blue accepts the complement language.

References

[1] Artur Jez, Anthony W. Lin, Oliver Markgraf, and Philipp R¨ummer. Decision proce-
dures for sequence theories. In Constantin Enea and Akash Lal, editors, Computer
Aided Verification - 35th International Conference, CAV 2023, Paris, France, July
17-22, 2023, Proceedings, Part II, volume 13965 of Lecture Notes in Computer Sci-
ence, pages 18–40. Springer, 2023.

[2] Diego Figueira and Anthony Widjaja Lin. Reasoning on data words over numeric
domains. In Christel Baier and Dana Fisman, editors, LICS ’22: 37th Annual
ACM/IEEE Symposium on Logic in Computer Science, Haifa, Israel, August 2 -
5, 2022, pages 37:1–37:13. ACM, 2022.

[3] Loris D’Antoni and Margus Veanes. The power of symbolic automata and transduc-
ers. In Rupak Majumdar and Viktor Kuncak, editors, Computer Aided Verification
- 29th International Conference, CAV 2017, Heidelberg, Germany, July 24-28, 2017,
Proceedings, Part I, volume 10426 of Lecture Notes in Computer Science, pages 47–
67. Springer, 2017.

[4] Orna Grumberg, Orna Kupferman, and Sarai Sheinvald. Variable automata over
infinite alphabets. In Adrian-Horia Dediu, Henning Fernau, and Carlos Mart??n-
Vide, editors, Language and Automata Theory and Applications, 4th International
Conference, LATA 2010, Trier, Germany, May 24-28, 2010. Proceedings, volume
6031 of Lecture Notes in Computer Science, pages 561–572. Springer, 2010.